Exercises – Long Day

Exercises – Long Day#

Exercise 1: Repetition Exercise on Recursion#

We recursively define a sequence of numbers $c_{0}, c_{1}, c_{2}, \dots$ as follows:

$c_{0} = 0$ , $c_{1} = 1$ , $c_{2} = 2$ , and for $n \geq 3$ it applies that $c_{n} = c_{n - 1} c_{n - 2} + c_{n - 3} .$

Which values do $c_{3}, c_{4}$ and $c_{5}$ have?

Answer

$c_{3} = c_{2} c_{1} + c_{0} = 2 \cdot 1 + 0 = 2$

$c_{4} = c_{3} c_{2} + c_{1} = 2 \cdot 2 + 1 = 5$

and

$c_{5} = c_{4} c_{3} + c_{2} = 5 \cdot 2 + 2 = 12.$

Question 2: Derivative Functions and Induction#

As is known from high-school, it applies for all $n \in Z_{\geq 1}$ that the derivative of $x^{n}$ is equal to $n x^{n - 1}$ , meaning $(x^{n})^{'} = n x^{n - 1}$ . In this exercise we will show this using induction. You may in this exercise use the fact that the derivative of $x$ is $1$ , as well as the product rule $(f (x) \cdot g (x))^{'} = f (x)^{'} \cdot g (x) + f (x) \cdot g (x)^{'} .$

Question a#

Formulate the base case of the induction. Then check that this base case holds.

Hint

Because we are showing that $(x^{n})^{'} = n x^{n - 1}$ for all $n \in Z_{\geq 1}$ , the base case of the induction is the case where $n = 1$ . So, substitute $n = 1$ into the equation $(x^{n})^{'} = n x^{n - 1}$ to see precisely what to check for in the base case of the induction.

Answer

The base case of the induction is the proposition that the formula $(x^{n})^{'} = n x^{n - 1}$ holds for $n = 1$ . In other words, the base case is the proposition $(x^{1})^{'} = 1$ . If one now uses the fact that $x^{1} = x$ , $x^{'} = 1$ and $x^{0} = 1$ , then the result follows after a few more computational steps.

Question b#

Now formulate the induction step. What is the induction hypothesis in this case?

Answer

The induction hypothesis is that the equation $(x^{n - 1})^{'} = (n - 1) x^{n - 2}$ holds true for any $n > 1$ .

Question c#

Show that the induction step holds. The induction principle now implies that the formula $(x^{n})^{'} = n x^{n - 1}$ holds true for all $n \in Z_{n \geq 1} .$

Hint

Note that $x^{n} = x^{n - 1} \cdot x$ . First explore what the product rule says if we choose $f (x) = x^{n - 1}$ and $g (x) = x$ . Then use the induction hypothesis.

Answer

The product rule combined with the induction hypothesis gives that $(x^{n})^{'} = (n - 1) x^{n - 2} \cdot x + x^{n - 1} \cdot 1 = n x^{n - 1}$ .

By the way, note that the formula $(x^{n})^{'} = n x^{n - 1}$ actually holds true for all real numbers $n$ and not only for natural numbers $n$ . Showing this is not a part of this exercise, though.

Exercise 3: The Sum of Odd Numbers and Induction#

Question a#

Compute for $n = 1, 2, 3, 4$ the sum of the first $n$ odd natural numbers. In other words, determine the value of $\sum_{k = 1}^{n} (2 k - 1)$ for $n \in {1, 2, 3, 4} .$ Is there a pattern in the values you find? Now try to find/guess a short expression of $\sum_{k = 1}^{n} (2 k - 1)$ that gives the correct result for $n \in {1, 2, 3, 4}$ and check that your guess also gives the correct value of $\sum_{k = 1}^{n} (2 k - 1)$ if $n = 5.$

Hint

The found values are always squares.

Answer

$\sum_{k = 1}^{1} (2 k - 1) = 1$ , $\sum_{k = 1}^{2} (2 k - 1) = 4$ , $\sum_{k = 1}^{3} (2 k - 1) = 9$ and $\sum_{k = 1}^{4} (2 k - 1) = 16$ .

Based on the above it is reasonable to guess that $\sum_{k = 1}^{n} (2 k - 1) = n^{2}$ is true for all $n$ . For $n = 5$ this guess also fits: $5^{2} = 25$ and $1 + 3 + 5 + 7 + 9 = 25$ .

Question b#

Let $P (n)$ be the logical proposition that $\sum_{k = 1}^{n} (2 k - 1)$ is equal to the short expression that you found in Question a. The goal is now to show that $P (n)$ is true for all natural numbers $n$ (that is, for all $n \in N = Z_{\geq 1}$ ).

Show that the base case of the induction holds.

Hint

The base case of the induction is the proposition $P (1)$ . In other words, to show that the base case holds, one must show that $P (1)$ is true.

Answer

$P (1)$ is the proposition that $\sum_{k = 1}^{1} (2 k - 1) = 1^{2}$ , but it holds true due to the work in Question a. In fact we know from Question a that $P (n)$ holds true for $n \in {1, 2, 3, 4, 5}$ , but in the base case of the induction one only has to check for $n = 1$ .

Question c#

Now carry out the induction step and then use the induction principle to conclude that $P (n)$ is true for all natural numbers $n$ .

Hint

In the induction step one must show for an arbitrary integer $n \geq 2$ that the implication $P (n - 1) \Rightarrow P (n)$ is true. In other words, in the induction step one must assume that $P (n - 1)$ is true and then from that show that $P (n)$ is also true.

Hint

For the induction step the recursive definition of the summation symbol given in Equation (5.5) in Chapter 5 of the textbook can be of good use.

Exercise 4: Multiplying into Parentheses#

Let $n \in Z_{\geq 2}$ and $a, b_{1}, \dots, b_{n}$ be complex numbers. Show the following using induction on $n$ :

a \cdot (b_{1} + \dots + b_{n}) = a \cdot b_{1} + \dots + a \cdot b_{n} .

You may use the fact that the equation holds true for $n = 2$ by refering to Theorem 3.2.2, part(iii).

Hint

The base case of the induction follows from Theorem 3.2.2 if you in this theorem choose $z_{1} = a$ , $z_{2} = b_{1}$ and $z_{3} = b_{2}$ .

Hint

For the induction step: $b_{1} + \dots + b_{n}$ can also be written as $\sum_{k = 1}^{n} b_{k}$ . Can Equation (5.5) from the textbook be of use?

Hint

From Equation (5.5) in the textbook we see that $\sum_{k = 1}^{n} b_{k} = (\sum_{k = 1}^{n - 1} b_{k}) + b_{n}$ . Hence it applies that

a \cdot (\sum_{k = 1}^{n} b_{k}) = a \cdot ((\sum_{k = 1}^{n - 1} b_{k}) + b_{n}) .

Can Theorem 3.2.2, part (iii), now be used to continue?

Opgave 5: The Geometric Series: part 1#

Spørgsmål a#

A bouncy ball is dropped from two metres above the floor. After hitting the floor, it bounces up one metre again before falling back to the ground. After hitting the floor the second time, it bounces up half a metre, then a quarter metre the third time, and so on. In other words, the fall height is halved with each impact with the floor.

Let $n$ be a natural number. What is the total distance the ball has traveled by the time it hits the floor for the $n$ ’th time?

Hint

After the first bounce, the ball has moved 2 metres, as it was dropped from 2 metres above the floor. By the second bounce, the total distance becomes $2 + 2 \cdot 1 = 4$ metres, since it rose 1 metre and then fell 1 metre. By the third bounce, the total distance increases to $2 + 2 \cdot (1 + \frac{1}{2})$ metres. After the fourth bounce, it becomes $2 + 2 \cdot (1 + \frac{1}{2} + \frac{1}{4})$ metres. Can you identify a pattern and express it using summation notation?

Svar

For $n = 1$ the answer is $2$ metres, for $n \geq 2$ the answer is $2 + 2 \cdot \sum_{j = 0}^{n - 2} \frac{1}{2^{j}} .$

Exercise 6: The Geometric Series: part 2#

Let $r \in C ∖ {1}$ be a complex number and $n$ a natural number. In this exercise we will show the following identity:

1 + r + \dots + r^{n} = \frac{r^{n + 1} - 1}{r - 1} .

Question a#

Why can $r$ not be equal to $1$ in the identity?

Answer

If $r = 1$ , then the denominator in the fraction $\frac{r^{n + 1} - 1}{r - 1}$ would become equal to zero. Hence the fraction is not defined for $r = 1$ .

Question b#

Check that the identity holds for $n = 1$ .

Hint

If we consider the expression $r^{2} - 1$ as a polynomial in the variable $r$ , then the polynomial has roots $1$ and $- 1$ . Now use Lemma 4.6.2 from the textbook to write $r^{2} - 1$ as a product of two first-degree polynomials.

Question c#

Show that the identity $1 + r + \dots + r^{n} = \frac{r^{n + 1} - 1}{r - 1}$ holds for all natural numbers $n$ .

Hint

Use induction on $n$ . Note that the base case of the induction was already handled in Question b.

Hint

The induction hypothesis is that $1 + r + \dots + r^{n - 1} = \frac{r^{n} - 1}{r - 1}$ . For the induction step, use that $1 + r + \dots + r^{n} = (1 + r + \dots + r^{n - 1}) + r^{n}$ and then the induction hypothesis.

Question d#

Let us return to the bouncy ball from Exercise 5. How many metres has the ball traversed in total before it lies still on the floor?

Hint

Choosing $r$ and $n$ in a smart way, you can simplify the expression you were asked to find in Exercise 5 using the identity

1 + r + \dots + r^{n} = \frac{r^{n + 1} - 1}{r - 1} .

What do you get when $n$ goes to infinity?

Svar

$6$ metres.

Exercise 7: An Inequality#

A sequence of real numbers $a_{0}, a_{1}, \dots$ is defined recursively as follows:

$a_{1} = 0$ and $a_{n} = \sqrt{2 + a_{n - 1}}$ if $n \geq 2$ .

Question a#

Compute $a_{1}, a_{2}, a_{3},$ and $a_{4}$ .

Answer

$a_{1} = 0$ , $a_{2} = \sqrt{2}$ , $a_{3} = \sqrt{2 + \sqrt{2}}$ , and $a_{4} = \sqrt{2 + \sqrt{2 + \sqrt{2}}} .$

If needed, numerically with many decimals:

$a_{1} = 0.00000000000000000000000000000$ .

$a_{2} = 1.41421356237309504880168872421$ .

$a_{3} = 1.84775906502257351225636637879$ .

$a_{4} = 1.96157056080646089825236447227$ .

Question b#

The claim is now that for all natural numbers $n$ it applies that $a_{n} < 2$ . Prove this using induction on $n$ .

Hint

For the induction step you may use the fact that the square root function $f : R_{\geq 0} \to R$ given by $x \mapsto \sqrt{x}$ is strictly increasing.

Exercise 8: A Sum with Fractions#

Show that the identity

\sum_{k = 1}^{n} \frac{1}{k (k + 1)} = 1 - \frac{1}{n + 1}

applies for all $n \in N .$

Exercise 9: Area under a Parabola#

Let $N$ be a positive real number and $n$ a natural number. We define $d = N / n$ . As is known from high-school, the area under the parabola (between the parabola and the first axis) from $x = 0$ to $x = N$ can be determined as follows:

\int_{0}^{N} x^{2} d x = \frac{1}{3} N^{3} - \frac{1}{3} 0^{3} = \frac{1}{3} N^{3} .

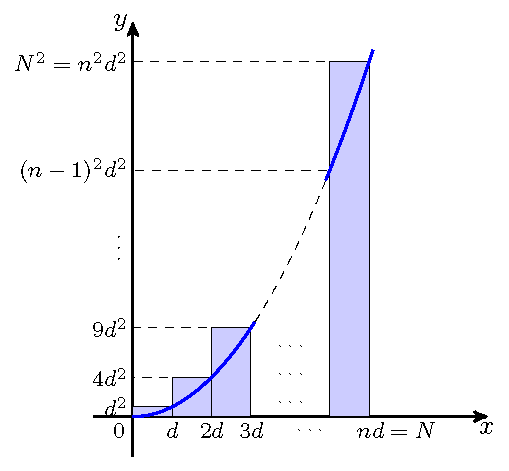
In this exercise we will investigate how well we can approximate this area by using the finite sum $\sum_{k = 1}^{n} d \cdot (k d)^{2}$ . The situation is illustrated in the following figure:

Question a#

Use the drawing to realise that

\frac{1}{3} N^{3} \leq \sum_{k = 1}^{n} d \cdot (k d)^{2} .

Question b#

Use the result from Exercise 4 to realise that

d^{3} \sum_{k = 1}^{n} k^{2} = \sum_{k = 1}^{n} d^{3} \cdot k^{2} = \sum_{k = 1}^{n} d \cdot (k d)^{2} .

Question c#

Use induction on $n$ to realise that $\sum_{k = 1}^{n} k^{2} = \frac{1}{3} n (n + 1 / 2) (n + 1)$ for all natural numbers $n$ .

Hint

With the induction step you will at some point reach the formula

\frac{1}{3} (n - 1) (n - 1 / 2) n + n^{2} .

You can of course multiply through and expand the expression to see if you get the correct result. But it can save you a lot of work to first bring $n$ outside of brackets:

\frac{1}{3} (n - 1) (n - 1 / 2) n + n^{2} = n (\frac{1}{3} (n - 1) (n - 1 / 2) + n) .

Now try to first realise that the expression within the brackets is equal to $\frac{1}{3} (n + 1 / 2) (n + 1) .$

Answer

The base case of the induction: If $n = 1$ , then the formula applies because $\sum_{k = 1}^{1} k^{2} = 1^{2} = 1$ and $\frac{1}{3} 1 (1 + 1 / 2) (1 + 1) = \frac{3}{3} = 1$ .

The induction step: If $n \geq 2$ , and if we assume the induction hypothesis that $\sum_{k = 1}^{n - 1} k^{2} = \frac{1}{3} (n - 1) (n - 1 / 2) n$ , then we arrive at

\sum_{k = 1}^{n} k^{2} = \sum_{k = 1}^{n - 1} k^{2} + n^{2} = \frac{1}{3} (n - 1) (n - 1 / 2) n + n^{2} .

For example, by following the above hint it should be possible to realise that $\frac{1}{3} (n - 1) (n - 1 / 2) n + n^{2} = \frac{1}{3} n (n + 1 / 2) (n + 1)$ , which means that the induction step holds. The induction principle hence implies that the formula $\sum_{k = 1}^{n} k^{2} = \frac{1}{3} n (n + 1 / 2) (n + 1)$ holds true for all natural numbers $n$ .

Question d#

Now show that $\sum_{k = 1}^{n} d \cdot (k d)^{2} = \frac{1}{3} N (N + d / 2) (N + d)$ .

Note: The equation implies that if $N$ is kept fixed, and if $n$ goes towards infinity, then $d$ goes towards zero and the sum thus goes towards $\frac{1}{3} N^{3},$ which is the area under the parabola.

Answer

From the previous questions we get

\sum_{k = 1}^{n} d \cdot (k d)^{2} = d^{3} \sum_{k = 1}^{n} k^{2} = d^{3} (\frac{1}{3} n (n + 1 / 2) (n + 1)) = \frac{1}{3} N (N + d / 2) (N + d) .

For the final equality we used that $N = d n$ .

Exercises – Long Day

Contents

Exercises – Long Day#

Exercise 1: Repetition Exercise on Recursion#

Question 2: Derivative Functions and Induction#

Question a#

Question b#

Question c#

Exercise 3: The Sum of Odd Numbers and Induction#

Question a#

Question b#

Question c#

Exercise 4: Multiplying into Parentheses#

Opgave 5: The Geometric Series: part 1#

Spørgsmål a#

Exercise 6: The Geometric Series: part 2#

Question a#

Question b#

Question c#

Question d#

Exercise 7: An Inequality#

Question a#

Question b#

Exercise 8: A Sum with Fractions#

Exercise 9: Area under a Parabola#

Question a#

Question b#

Question c#

Question d#